📊 Analisis Algoritma
dan Kompleksitas
Struktur Data dan Algoritma
Pertemuan 02
Universitas Pertahanan RI
🎯 Tujuan Pembelajaran
Setelah pertemuan ini, mahasiswa mampu:
- Menjelaskan pentingnya analisis algoritma
- Menghitung kompleksitas waktu menggunakan notasi Big-O
- Membedakan notasi Big-O, Big-Ω, dan Big-Θ
- Menganalisis best case, worst case, dan average case
- Mengidentifikasi kelas-kelas kompleksitas umum
- Menganalisis kompleksitas algoritma iteratif dan rekursif
📋 Agenda
Bagian 1
- Mengapa Analisis Penting?
- Menghitung Operasi Dasar
- Notasi Asimptotik
- Aturan Penyederhanaan
Bagian 2
- Kelas Kompleksitas Umum
- Best/Worst/Average Case
- Analisis Iteratif
- Analisis Rekursif
- Master Theorem
📖 1. Mengapa Analisis Algoritma Penting?
Algoritma adalah urutan langkah-langkah komputasi yang terdefinisi dengan baik untuk menyelesaikan suatu masalah dalam waktu terbatas.
🎖️ Contoh: Database Personel Militer
Dua algoritma untuk mencari data dari 1 juta personel:
Algoritma A
1 detik
untuk 1 juta data
Algoritma B
1 jam
untuk 1 juta data
Keduanya benar, tapi perbedaan 3600× lebih lambat!
Dalam operasi pertahanan, keterlambatan = risiko fatal.
Faktor yang Mempengaruhi Waktu Eksekusi
- Kecepatan hardware (CPU, RAM, storage)
- Bahasa pemrograman dan compiler
- Kualitas implementasi (coding style)
- Ukuran input (n)
- Algoritma yang digunakan ← Fokus analisis!
Analisis algoritma fokus pada faktor ke-5 karena dapat dikontrol programmer terlepas dari hardware.
Empiris vs Teoritis
| Aspek | Analisis Empiris | Analisis Teoritis |
|---|---|---|
| Metode | Mengukur waktu aktual | Menghitung operasi dasar |
| Ketergantungan HW | Tinggi | Tidak ada |
| Input | Harus ada data aktual | Untuk semua ukuran n |
| Hasil | Waktu (ms/detik) | Fungsi pertumbuhan |
📖 2. Menghitung Operasi Dasar
Operasi dasar adalah instruksi komputasi yang diasumsikan membutuhkan waktu konstan, terlepas dari ukuran input.
- Operasi aritmatika: +, -, *, /, %
- Operasi perbandingan: <, >, ==, !=
- Assignment: =
- Akses elemen array dengan indeks
💻 Contoh Penghitungan Operasi
int findMax(int arr[], int n) {
int max = arr[0]; // 2 operasi
for (int i = 1; i < n; i++) { // 1 + (n-1) + (n-1) operasi
if (arr[i] > max) { // 2 operasi per iterasi
max = arr[i]; // 2 operasi (worst case)
}
}
return max; // 1 operasi
}
Total (worst case): 2 + 1 + (n-1) + (n-1) + 2(n-1) + 2(n-1) + 1 = 6n - 2
🧠 Quiz: Hitung Operasi
int sum = 0;
for (int i = 0; i < n; i++) {
sum = sum + arr[i];
}
Berapa total operasi dasar?
int sum = 0 | 1 |
i < n | n+1 |
i++ | n |
arr[i], sum + ..., sum = ... | 3n |
Total = 1 + 1 + (n+1) + n + 3n = 5n + 3
📖 3. Notasi Asimptotik
Konsep Pertumbuhan Fungsi
Untuk n sangat besar, hanya suku dengan pangkat tertinggi yang dominan:
T(n) = 3n² + 5n + 100
n = 1000: 3(1.000.000) + 5000 + 100 = 3.005.100
Suku n² mendominasi ~99.8% dari total!
Big-O (Upper Bound)
Definisi: f(n) = O(g(n)) jika terdapat konstanta positif c dan n₀ sehingga f(n) ≤ c·g(n) untuk semua n ≥ n₀
Gambar 2.1: Visualisasi Big-O — f(n) dibatasi oleh c·g(n) untuk n ≥ n₀
Perbandingan Notasi
| Notasi | Analogi | Makna |
|---|---|---|
| O(g(n)) | ≤ | Batas atas (upper bound) |
| Ω(g(n)) | ≥ | Batas bawah (lower bound) |
| Θ(g(n)) | = | Batas ketat (tight bound) |
Dalam praktik, Big-O paling sering digunakan karena memberikan garansi worst case.
🧠 Quiz: Buktikan Big-O
Buktikan bahwa 3n² + 5n + 100 = O(n²)
Langkah: Untuk n ≥ 1:
- 5n ≤ 5n²
- 100 ≤ 100n²
3n² + 5n + 100 ≤ 3n² + 5n² + 100n² = 108n²
Dengan c = 108 dan n₀ = 1, terbukti. ∎
📖 4. Aturan Penyederhanaan Big-O
Aturan Konstanta
O(c·f(n)) = O(f(n))
Contoh: O(5n) = O(n)
Aturan Suku Dominan
O(f + g) = O(max(f, g))
Contoh: O(n² + n) = O(n²)
Aturan Penjumlahan (Sum Rule)
Untuk dua segmen kode berurutan:
// Segmen 1: O(n)
for (int i = 0; i < n; i++) { /* ... */ }
// Segmen 2: O(n²)
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) { /* ... */ }
}
// Total: O(n + n²) = O(n²)
T(n) = T₁(n) + T₂(n) → O(max(T₁, T₂))
Aturan Perkalian (Product Rule)
Untuk loop bersarang:
// Loop luar: n kali
for (int i = 0; i < n; i++) {
// Loop dalam: n kali per iterasi
for (int j = 0; j < n; j++) {
/* O(1) operation */
}
}
// Total: O(n × n) = O(n²)
T(n) = T₁(n) × T₂(n) → O(T₁ × T₂)
🧠 Quiz: Sederhanakan
Sederhanakan: O(3n³ + 100n² + n + 5000)
- Identifikasi suku dominan: 3n³ (tumbuh paling cepat)
- Aturan suku dominan: O(3n³ + 100n² + n + 5000) = O(3n³)
- Aturan konstanta: O(3n³) = O(n³)
📖 5. Kelas-Kelas Kompleksitas Umum
| Notasi | Nama | Contoh Algoritma |
|---|---|---|
| O(1) | Konstanta | Akses array dengan indeks |
| O(log n) | Logaritmik | Binary search |
| O(n) | Linear | Linear search |
| O(n log n) | Linearitmik | Merge sort, Quick sort |
| O(n²) | Kuadratik | Bubble sort |
| O(2ⁿ) | Eksponensial | Brute force subset |
Perbandingan Pertumbuhan
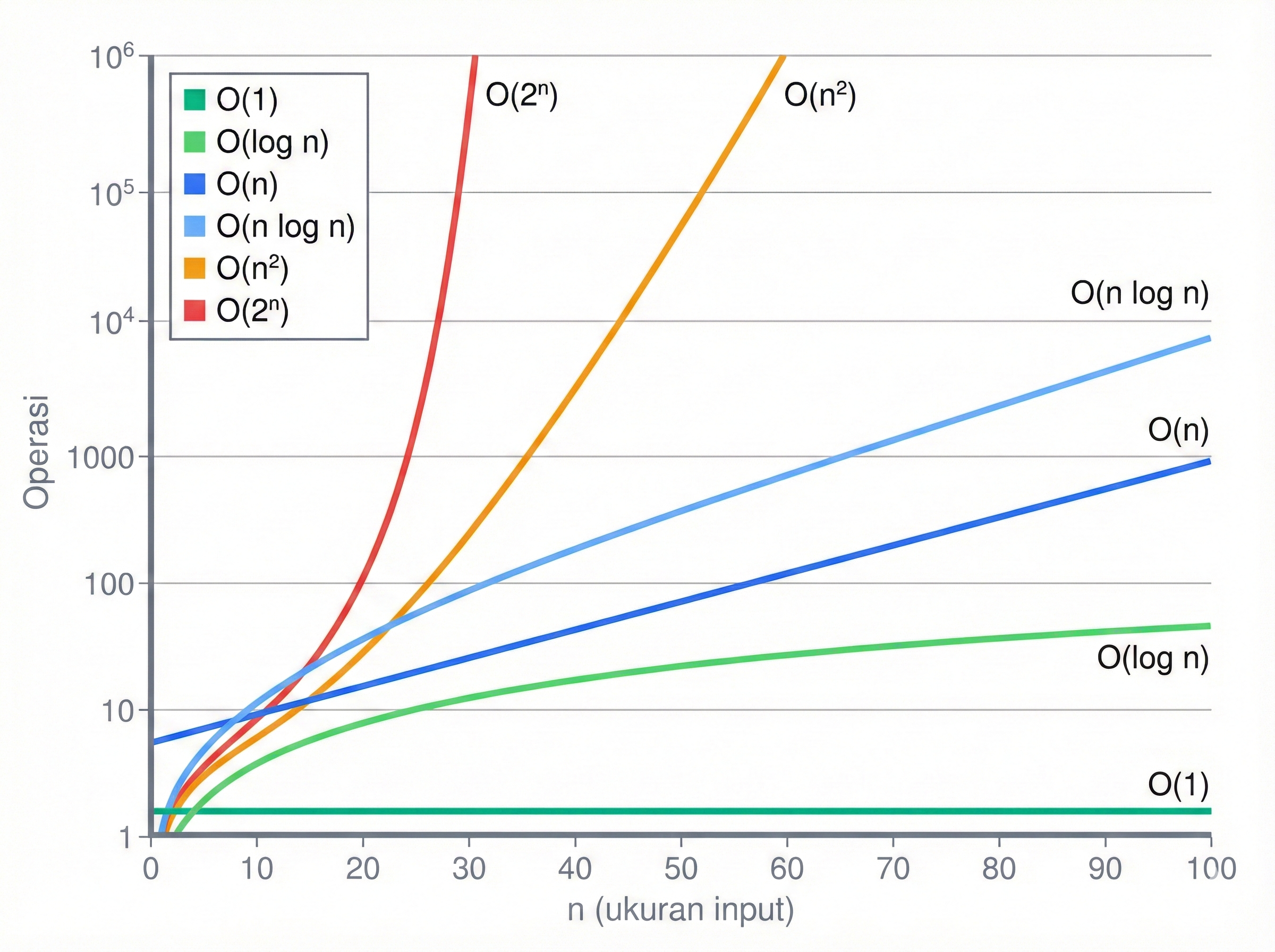
Gambar 2.2: Perbandingan pertumbuhan berbagai kelas kompleksitas
Dampak Praktis (10⁹ ops/sec)
| n | O(log n) | O(n) | O(n log n) | O(n²) | O(2ⁿ) |
|---|---|---|---|---|---|
| 10 | 3 ns | 10 ns | 33 ns | 100 ns | 1 μs |
| 100 | 7 ns | 100 ns | 664 ns | 10 μs | 10¹⁴ tahun! |
| 10⁶ | 20 ns | 1 ms | 20 ms | 17 menit | ∞ |
| 10⁹ | 30 ns | 1 detik | 30 detik | 31 tahun | ∞ |
Untuk n besar, algoritma eksponensial praktis tidak dapat diselesaikan!
🎖️ Analogi Militer
| Kompleksitas | Analogi Verifikasi Identitas |
|---|---|
| O(1) | Periksa badge ID elektronik — langsung |
| O(log n) | Cari di buku registrasi terurut |
| O(n) | Panggil absen satu per satu |
| O(n²) | Setiap orang menyalami semua orang lain |
| O(2ⁿ) | Evaluasi semua kombinasi tim — tidak praktis! |
📖 6. Best, Worst, Average Case
Untuk input berukuran n yang sama, waktu eksekusi bisa berbeda tergantung konfigurasi input.
Best Case
Waktu minimum
Worst Case
Waktu maksimum
Average Case
Waktu rata-rata
Contoh: Linear Search
int linearSearch(int arr[], int n, int key) {
for (int i = 0; i < n; i++) {
if (arr[i] == key) return i; // Ditemukan
}
return -1; // Tidak ditemukan
}
| Case | Kondisi | Kompleksitas |
|---|---|---|
| Best | Key di posisi pertama | O(1) |
| Worst | Key tidak ada / di akhir | O(n) |
| Average | Key di posisi acak | O(n) |
Mana yang Paling Penting?
Dalam praktik, worst case paling sering digunakan karena memberikan garansi performa.
Kita bisa yakin algoritma tidak akan lebih lambat dari batas worst case.
Average case berguna untuk algoritma yang worst case-nya jarang terjadi (seperti Quick Sort).
📖 7. Analisis Algoritma Iteratif
Pola Loop Tunggal
// Pola 1: Loop linear
for (int i = 0; i < n; i++) { ... } // O(n)
// Pola 2: Loop dengan increment konstan
for (int i = 0; i < n; i += 2) { ... } // O(n/2) = O(n)
// Pola 3: Loop dengan pengali
for (int i = 1; i < n; i *= 2) { ... } // O(log n)
// Pola 4: Loop dengan pembagi
for (int i = n; i > 0; i /= 2) { ... } // O(log n)
Pola Loop Bersarang
// Pola 1: Nested linear → O(n²)
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) { ... }
}
// Pola 2: Loop dalam bergantung pada i → O(n²)
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) { ... }
}
// Total: 0+1+2+...+(n-1) = n(n-1)/2 = O(n²)
// Pola 3: Loop luar logaritmik → O(n log n)
for (int i = 1; i < n; i *= 2) {
for (int j = 0; j < n; j++) { ... }
}
🧠 Quiz: Kompleksitas Mystery
void mystery(int n) {
for (int i = 1; i < n; i = i * 2) {
for (int j = 0; j < n; j++) {
cout << i << " " << j << endl;
}
}
}
Tentukan kompleksitas waktu!
- Loop luar: i dikali 2 → O(log n)
- Loop dalam: j dari 0 sampai n → O(n)
Total: O(log n) × O(n) = O(n log n)
📖 8. Analisis Algoritma Rekursif
Recurrence Relation
void printN(int n) {
if (n <= 0) return; // Base case
cout << n << endl; // O(1)
printN(n - 1); // T(n-1)
}
Relasi rekurens:
T(0) = 1 (base case)
T(n) = T(n-1) + 1 (untuk n > 0)
Metode Substitusi
Selesaikan T(n) = T(n-1) + 1, T(0) = 1:
T(n) = T(n-1) + 1
T(n) = [T(n-2) + 1] + 1 = T(n-2) + 2
T(n) = [T(n-3) + 1] + 2 = T(n-3) + 3
...
T(n) = T(n-k) + k
Ketika k = n: T(n) = T(0) + n = 1 + n = O(n)
Fibonacci Rekursif (Naive)
long fib(int n) {
if (n <= 1) return n;
return fib(n-1) + fib(n-2); // Dua pemanggilan rekursif!
}
Relasi rekurens: T(n) = T(n-1) + T(n-2) + c
Solusi: T(n) ≈ O(2ⁿ) — Sangat tidak efisien!
Pohon Rekursi Fibonacci
Gambar 2.3: Pohon rekursi Fibonacci — banyak perhitungan redundan
Contoh: Binary Search Rekursif
Relasi: T(n) = T(n/2) + c, T(1) = c
T(n) = T(n/2) + c
T(n) = T(n/4) + c + c = T(n/4) + 2c
...
T(n) = T(n/2^k) + k·c
Ketika n/2^k = 1 → k = log₂(n):
T(n) = c + c·log₂(n) = O(log n)
📖 9. Master Theorem
Untuk relasi rekurens divide-and-conquer:
T(n) = aT(n/b) + nd
a ≥ 1: jumlah subproblem | b > 1: faktor pembagi | d ≥ 0: waktu merge
Kasus Master Theorem
| Kondisi | Kompleksitas |
|---|---|
| a < bd | O(nd) |
| a = bd | O(nd log n) |
| a > bd | O(nlogba) |
Contoh Penerapan
Merge Sort:
T(n) = 2T(n/2) + n
a=2, b=2, d=1 → bd=2
a = bd → O(n log n)
Binary Search:
T(n) = T(n/2) + 1
a=1, b=2, d=0 → bd=1
a = bd → O(log n)
🧠 Quiz: Master Theorem
Selesaikan: T(n) = 3T(n/2) + n
- a = 3, b = 2, d = 1
- bd = 21 = 2
- a = 3 > 2 = bd → Kasus ketiga
T(n) = O(nlog₂3) ≈ O(n1.585)
📝 Ringkasan
| Topik | Poin Kunci |
|---|---|
| Big-O | Batas atas (upper bound): f(n) ≤ c·g(n) |
| Big-Ω | Batas bawah (lower bound): f(n) ≥ c·g(n) |
| Big-Θ | Batas ketat: Big-O dan Big-Ω sama |
| Aturan Sum | O(f + g) = O(max(f, g)) |
| Aturan Product | O(f × g) = O(f) × O(g) |
| Worst Case | Memberikan garansi performa maksimum |
| Master Theorem | T(n) = aT(n/b) + nd, bandingkan a dengan bd |
📊 Hierarki Efisiensi
| Kompleksitas | Nama | Efisiensi |
|---|---|---|
| O(1) | Konstanta | ⭐⭐⭐⭐⭐ |
| O(log n) | Logaritmik | ⭐⭐⭐⭐ |
| O(n) | Linear | ⭐⭐⭐ |
| O(n log n) | Linearitmik | ⭐⭐⭐ |
| O(n²) | Kuadratik | ⭐⭐ |
| O(2ⁿ) | Eksponensial | ⭐ |
| O(n!) | Faktorial | ☆ |
❓ Pertanyaan?
Silakan bertanya atau diskusi
Referensi: Cormen Ch.2-3 | Weiss Ch.2 | Goodrich Ch.4
Terima Kasih! 🙏
Struktur Data dan Algoritma
Pertemuan 02
© 2026 - CC BY 4.0